Intro to Finance & Options (STEMS 2024)

Table of Contents

Link to the STEMS 2024 website: https://tessellate.cmi.ac.in/stems/
Link to the Tessellate 2024 website: https://tessellate.cmi.ac.in/

Finance 101

Time Value of Money & Present Value

• Money today is worth more than the same amount of money in the future. This is due to the potential for earning interest over time.

• Present Value (PV): The current worth of a future sum of money, discounted back to the present using a specific interest rate. This helps compare future cash flows to their present value for investment decisions.

• Discount rate: The interest rate used to discount future cash flows back to their present value.

  $$\text{PV} = \frac{\text{Future Value}}{(1 + \text{Discount Rate})^{\text{Time}}}$$

Cash Flows

• A cash flow is any movement of money into or out of an entity (e.g., individual, company). It can be:
  • Positive: Receiving money (income, investment returns)
  • Negative: Spending money (expenses, loan payments)

No-Arbitrage Principle

• Arbitrage:
  • Taking advantage of price discrepancies between equivalent assets in different markets to make a risk-free profit. This profit arises from exploiting temporary inefficiencies in market pricing.
• Necessary Conditions for Arbitrage:
  • Price discrepancy: There must be a difference in the price of the same or equivalent assets in different markets. This difference cannot be justified by fundamental factors like risk or liquidity.
  • Risk-free: The arbitrage opportunity must be guaranteed to make a profit without any risk of loss. This means there are no transaction costs, execution risks, or potential changes in prices before you can exploit the discrepancy.
  • Replicability: The arbitrage opportunity must be replicable by other investors.This ensures that the price discrepancy will be quickly eliminated, restoring market efficiency.
• In efficient markets, equivalent assets should have the same risk-adjusted return.
  • If an arbitrage opportunity exists, investors will take advantage of it, eliminating the price discrepancy, ensuring market efficiency and fair pricing of assets.

Need for Options

• Consider a situation where you are uncertain about the price of a good you are selling.

  You need to sell each unit for a minimum of $\operatorname{Rs.} 40$ to cover your costs, and you need to sell at least $100$ units by the end of the month. You find someone who is willing to accept this deal, if you decide to execute it, but they ask for $\operatorname{Rs.}10$ to give you this option.

  Thus, for $\operatorname{Rs.}10$, you get the choice to sell a fixed quantity of your good, at the fixed price. If you choose to execute this deal, you get the $\operatorname{Rs.}4000$ at the end of the month. If you don’t execute this deal, you get nothing, and your $\operatorname{Rs.}10$ will not be refunded.

• Now consider the opposite situation, where you are uncertain about the quantity of a good you will need a month from now.

  You need to at least $100$ units by the end of the month, and you are willing to pay $\operatorname{Rs.}40$ for each unit. You find someone who is willing to accept this deal, if you decide to execute it, but they ask for $\operatorname{Rs.}10$ to give you this option.

  Thus, for $\operatorname{Rs.}10$, you get the choice to buy a fixed quantity of the required good, at the fixed price. If you choose to execute this deal, you will have to pay the $\operatorname{Rs.}4000$ at the end of the month. If you don’t execute this deal, you get nothing, and your $\operatorname{Rs.}10$ will not be refunded.

• This contract can be thought of as an insurance in both cases - insuring the minimum sales and the available quantity respectively.

Value Proposition

The value of such a contract lies in the fact that you are not obligated to exercise it. If you are able to sell a good at a higher price, or if you are able to buy the good for a lower price, you can let the contract expire, and your downside is limited to the price of the contract.

Definitions

• Call Option: A type of option contract that allows the holder to buy an asset at a specified price, known as the strike price, on a specified future date, known as the expiration date. The holder is not obligated to buy the asset; they have the right to do so.
• Put Option: A type of option contract that allows the holder to sell an asset at a specified price on a specified future date, known as the expiration date. Again, the holder is not obligated to sell the asset; they have the right to do so.

(These are the European definitions. American Options are slightly different in that they allow you you to exercise the option any time before the expiration date.)

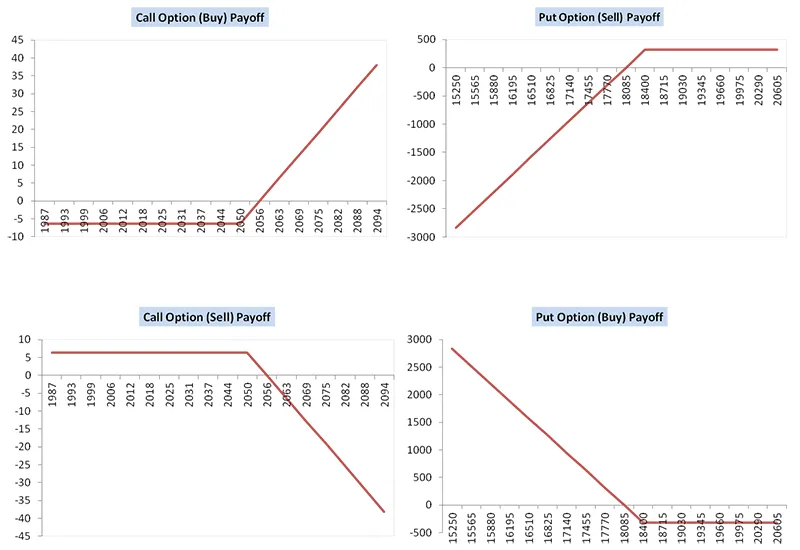
Payoff structures

• Consider that you buy a call option over a stock, with a strike price of $\operatorname{Rs.}10$, for $c$.

  • Situation 1:

    At the time of expiry, the value of the stock is $\operatorname{Rs.}20$. So, you exercise your call option to buy the stock at $\operatorname{Rs.}10$ and you immediately sell it in the market for $\operatorname{Rs.}20$, giving you a profit of $\operatorname{Rs.}10 - c$.

  • Situation 2:

    At the time of expiry, the value of the stock is $\operatorname{Rs.}5$. So, you let your call option expire, leaving you with a loss of $c$.

  Thus, your pay-off is given by

  $$P = \max(S - K, 0) - c$$

  where,

  • $P$ - Profit
  • $S$ - price of the underlying security at expiry
  • $K$ - strike price
  • $c$ - price of the call option

• Similarly, we get that if you buy a put option, your pay-off is given by

  $$P = \max(K - S, 0) - p$$

  where,

  • $P$ - Profit
  • $S$ - price of the underlying security at expiry
  • $K$ - strike price
  • $p$ - price of the put option

• Now what if instead of buying an option, you sell an option?

  in an abstract, purely mathematical sense, selling is the same as buying a negative amount. Thus, the pay-offs in this case will be the negative of the respective cases.

  • You get paid initially for selling the option and then depending on the value of the stock at maturity, you lose the amount that is profited by the person exercising the option.

  (Selling an option is often referred to as shorting an option. The accurate definition of here.)

Thus, the pay-off diagrams for all the option look like

Combinations of Options

• In a portfolio with multiple options, they can simply super-impose the pay-off diagrams of the options expiring at the same time.

• This idea can be compared to the super-imposition of sine waves to get approximations for a function in Fourier Transforms.

  Extending the idea, we can use options to approximate a cash flow at a particular time. Putting all such option approximations of cash flows at different times in the same portfolio, we get an approximation for the original portfolio.

  Of course, this is not always true, but it is a very interesting notion, drawing a comparison between portfolio construction and Fourier Transformations.